nutate.c File Reference

Correct for nutation. More...

#include <math.h>
#include <stdlib.h>
#include "aephem.h"

Macros
#define	ae_mod_3600(x)   ((x) - 1296000. * floor ((x)/1296000.))
	A handy macro.

Functions
void	ae_nut_sscc (int k, double arg, int n)
	Do trigonometric calculations for ae_nutation_lon_ob().
void	ae_nutation_lon_ob (double jd_tt, double *nutl, double *nuto)
	Calculate the nutation in longitude and oblation. More...
void	ae_nutate (double nutl, double nuto, double eps, double p[], int direction)
	Correct for nutation. More...
void	aes_nutate (double jd_tt, double p[], int direction)
	Correct for nutation. More...

Variables
short	ae_nt_param [105 *9]
	Nutation parameters. More...
double	ae_nut_ss [5][8]
	An array to hold the sine of multiple angles.
double	ae_nut_cc [5][8]
	An array to hold the cosine of multiple angles. More...

Detailed Description

Correct for nutation.

Function Documentation

void ae_nutate	(	double	nutl,
		double	nuto,
		double	eps,
		double	p[],
		int	direction
	)

Correct for nutation.

From AA page B20.

Parameters

nutl	The nutation in longitude in seconds of arc (see ae_nutation_lon_ob()).
nuto	The nutation in oblation in seconds of arc (see ae_nutation_lon_ob()).
eps	The obliquity of the ecliptic in seconds of arc (see ae_epsilon()).
p	The equitorial rectangular position vector for mean ecliptic and equinox of date. This is modified by the routine for nutation.
direction	AE_TO_J2000 to nutate from jd_tt to J2000; AE_FROM_J2000 to nutate from J2000 to jd_tt. (If neither is passed, AE_TO_J2000 is assumed.) To nutate from jd_1 to jd_2, first go from jd_1 to J2000, and then from J2000 to jd_2.

References AE_FROM_J2000, and AE_STR.

Referenced by ae_geocentric_moon_from_orbit(), and aes_nutate().

void ae_nutation_lon_ob	(	double	jd_tt,
		double *	nutl,
		double *	nuto
	)

Calculate the nutation in longitude and oblation.

References:

• "Summary of 1980 IAU Theory of Nutation (Final Report of the IAU Working Group on Nutation)", P. K. Seidelmann et al., in Transactions of the IAU Vol. XVIII A, Reports on Astronomy, P. A. Wayman, ed.; D. Reidel Pub. Co., 1982.
• "Nutation and the Earth's Rotation", I.A.U. Symposium No. 78, May, 1977, page 256. I.A.U., 1980.
• Woolard, E.W., "A redevelopment of the theory of nutation", The Astronomical Journal, 58, 1-3 (1953).

This program implements all of the 1980 IAU nutation series. Results checked at 100 points against the 1986 AA; all agreed.

Parameters

jd_tt	The Julian date in TT.
nutl	For returning the nutation in longitude, in seconds of arc.
nuto	For returning the nutation in oblation, in seconds of arc.

References ae_mod_3600, ae_nt_param, ae_nut_cc, ae_nut_ss, ae_nut_sscc(), and AE_STR.

Referenced by ae_geocentric_moon_from_orbit(), ae_topocentric(), aes_last(), and aes_nutate().

void aes_nutate	(	double	jd_tt,
		double	p[],
		int	direction
	)

Correct for nutation.

This is a simplified version of ae_nutate(), which automatically calculates nutl, nuto and eps. It might be less efficient to use this routine if speed is required.

Parameters

jd_tt	The Julian date in TT.
p	The equitorial rectangular position vector for mean ecliptic and equinox of date. This is modified by the routine for nutation.
direction	AE_TO_J2000 to nutate from jd_tt to J2000; AE_FROM_J2000 to nutate from J2000 to jd_tt. (If neither is passed, AE_TO_J2000 is assumed.) To nutate from jd_1 to jd_2, first go from jd_1 to J2000, and then from J2000 to jd_2.

References ae_epsilon(), ae_nutate(), and ae_nutation_lon_ob().

Referenced by ae_geocentric(), ae_geocentric_from_cat(), and ae_phys_pole().

Variable Documentation

short ae_nt_param[105 *9]

Nutation parameters.

Each term in the expansion has a trigonometric argument given by

where the variables are defined below. The nutation in longitude is a sum of terms of the form 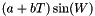. The terms for nutation in obliquity are of the form 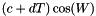. The coefficients are arranged in the tabulation as follows:

i	j	k	l	m	a	b	c	d
0	0	0	0	1	-171996	-1742	92025	89

The first line of the table, above, is done separately since two of the values do not fit into 16 bit integers. The values a and c are arc seconds times 10000. B and d are arc seconds per Julian century times 100000. I through m are integers. See the program for interpretation of MM, MS, etc., which are mean orbital elements of the Sun and Moon.

If terms with coefficient less than X are omitted, the peak errors will be:

omit a <	error, longitude	omit c <	error, obliquity
.0005"</td><td>.0100"	.0008" </td><td> .0094"
.0046	.0492	.0095	.0481
.0123	.0880	.0224	.0905
.0386	.1808	.0895	.1129

Referenced by ae_nutation_lon_ob().

double ae_nut_cc[5][8]

An array to hold the cosine of multiple angles.

Referenced by ae_nut_sscc(), and ae_nutation_lon_ob().