About

AEPHEM is an astronomical ephemeris and reduction C library, along with python bindings. Orbital information can be taken from built-in perterbation tables for major Solar System objects, JPL ephemerides (which need to be downloaded seperately) and Keplerian orbital elements.

Routines allow for reduction to geocentric and topocentric equatorial coordinates and can correct for: precession, annual and diurnal aberration, annual and diurnal parallax, nutation, light travel time, light deflection and atmospheric refraction (in both optical and millimetre/sub-millimetre). Sub-observer points can also be calculated.

Calendar routines allow for conversion between calendar time, UNIX time, sidereal time and Julian Dates, and offsets between Universal Coordinated Time (UTC), Universal Time (UT1) and Terrestrial Time (TT) are readily calculated.

Routines for transforming from equitorial to horizontal and galactic coordinates are also provided.

AEPHEM is based on AA, by Stephen L. Moshier, available at http://www.moshier.net/. Most algorithms are taken from the Astronomical Almanac, and references for each function are provided in these help pages. The functions for parsing binary JPL ephemerides are based on the JPL DE ephemerides code of Project Pluto, released under the GNU General Public Licencee.

AEPHEM is free software; you can redistribute it and/or modify it under the terms of the GNU General Public Licence as published by the Free Software Foundation; either version 3 of the Licence, or (at your option) any later version.

Introduction

An ephemeris (pl. ephemerides) gives the positions of Solar System bodies at series of times. These are generally in heliocentric, rectangular coordinates. Between the tabulated times one can must interpolate, and a good ephemeris will provide coefficients for precise interpolation formulae. A much less precise way to determine positions is by using Kepler's Laws given basic orbital elements. A balance between these two methods, which is good enough for many applications, is to store tables of coefficients for calculating perturbations from Keplerian orbits due to the influences of the planets. AEPHEM can use all of three of these methods: it can read in JPL ephemerides, it has built-in perturbation coefficients, and it can use Kepler's Laws — see Ephemerides and Orbital Elements.

Reducing the rectangular, heliocentric coordinates to an apparent altitude and azimuth on the surface of the earth is a subtle process requiring several corrections. The functions that perform the reductions are described in Astrometric Reductions.

Quick Example

#include <aephem.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define LATITUDE    -12.345     // Degrees north of the equator. 
#define LONGITUDE   -67.890     // Degrees east of the meridean.
#define ALTITUDE    5200        // Metres above sea level.
int main(int argc, char *argv[]) {
  double jd_ut, jd_ut1, jd_tt, last, ra, dec, dist, alt, az;
  jd_ut = ae_ctime_to_jd(time(NULL));  // Current Julian date in UT measure.
  jd_ut1 = jd_ut + ae_dut1(jd_ut) * AE_D_PER_S;     // UT1 measure.
  jd_tt = jd_ut1 + ae_delta_t(jd_ut1) * AE_D_PER_S; // TT measure.
  last = aes_last(jd_ut1, LONGITUDE);   // Local apparent sidereal time.
  // Get the geocentric ra/dec of Mars.
  ae_geocentric_from_orbit(jd_tt, &ae_orb_earth, &ae_orb_mars, &ra, &dec,
                           &dist);
  // Get the apparent ra/dec of Mars (no atmospheric model).
  aes_topocentric(jd_ut1, LATITUDE, LONGITUDE, dist, &ra, &dec);
  // Convert to alt/az.
  ae_radec_to_altaz(last, LATITUDE, ra, dec, &alt, &az);
  printf("JD (UT1) = %.5f, JD (TT) = %.5f\n", jd_ut1, jd_tt);
  printf("Apparent ra/dec of Mars = " ae_hms_fmt ", " ae_dms_fmt "\n",
         ae_hms_arg(ra),
         ae_dms_arg(dec));
  printf("Az/alt of Mars = " ae_dms_fmt ", " ae_dms_fmt "\n", 
         ae_dms_arg(az), ae_dms_arg(alt));
  return 0;
}

Compile with: gcc -o quick_example quick_example.c -laephem -lm

Conventions

Functions in AEPHEM all begin with the prefix ae_ or aes_. The latter prefix indicates a "simplified" function which requires fewer arguments but may sacrifice flexibility or efficiency.

Global variables also begin with the prefix ae_; similarly, constants (defined as preprocessor macros) begin with AE_.

Units

Angles: All functions accept and return angles in degrees. This means that many routines internally need to convert to radians and back, but this is a small inefficiency worth paying for consistency and clarity. The following exceptions to this rule are:
- Nutation in longitude and obliquity are in seconds of arc (c.f. ae_epsilon(), ae_nutation_lon_ob()).
- Catalogue objects' proper motions are in seconds of arc per century; in the input star catalogues, proper motions in right ascension are written in seconds per century.
- In input star catalogues, right ascensions are written in hours, as is customary.
Distances: In general, distances are measured in astronomical units (AU).
- The function ae_geocentric_lat() accepts the altitude in metres.
- Distances from the centre of the earth are measured in earth radii, i.e., AE_R_EARTH (e.g., ae_diurnal_aberration(), ae_diurnal_parallax()).
Speeds: Speeds are measured in AU per day.
- Radial velocities in ae_star_t objects, and star catalogues, are in kilometres per second.

Here are some useful constants for converting between units:

For angle conversions: AE_DTR, AE_RTD, AE_RTS, AE_STR, AE_STD.
For distance conversions: AE_AU, AE_R_EARTH, AE_R_EARTH_AU.
For speed conversions: AE_CLIGHT, AE_CLIGHT_AUD.

Dates and Times

Most functions accept the date and time in the form of the fractional Julian date (JD). This is the number of days elapsed since noon Universal Time Monday, January 1, 4713 BC, in the Julian calendar. The following functions can be used to find Julian dates:

ae_cal_to_jd() — for converting a regular calendar date to a JD;
ae_ctime_to_jd() — for converting a UNIX time to a JD.

Some functions require the local apparent sidereal time (LAST). In AEPHEM, LAST is always passed and returned in units of degrees. The LAST is the sidereal time at the geographical location of the observer, hence "local". It has also been corrected for nutation so that the true length of the day is used, hence "apparent", as opposed to mean sidereal time (MST), which uses the mean length of the day. Routines for calculating the LAST, and other sidereal times are:

ae_ctime_to_last() — for converting a UNIX time to the LAST;
aes_ctime_to_last() — a simplified version of ae_ctime_to_last();
ae_last() — for converting a Julian date to the LAST;
aes_last() — a simplified version of ae_last();
ae_lmst() — for converting a Julian date to the LMST;
ae_gast() — for converting a Julian date to the LAST at the Greenwich meridian;
ae_gmst() — for converting a Julian date to the LMST at the Greenwich meridian.

There are several time scales pertinent to ephemerides and astronomical reductions. This is necessary because the length of the day varies as tidal forces alter the earth's rotation. The day is lengthening by about a second every two years, though on shorter time scales the rotational period is variable and difficult to predict. The different timescales are designed to cope with this erratic behaviour for different applications. The important ones for AEPHEM are:

UTC (Universal Coordinated Time) — This is the standard, every-day time at the zero longitude meridian. It is what is generally reported by GPS devices. The length of the second is fixed and leap seconds are added when necessary to keep UTC to within 0.9 seconds of UT1.
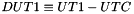UT1 — This is the true time. The sun transits at exactly noon at the zero longitude meridian in UT1. UT1 varies daily. UTC is kept to within 0.9 seconds of UT1. The difference between the two is defined as $DUT1 \equiv UT1 - UTC$ .
TT (Terrestrial Time) — Terrestrial Time has a second that is the same length as UT, but does not add leap seconds. Consequently, the difference between UT1 and TT is growing. The difference between the two is defined as 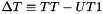$\Delta T \equiv TT - UT1$ . TT is used in ephemerides.

In AEPHEM, function prototypes indicate which timescale is expected by appending a lower-case suffix, i.e., jd_utc, jd_ut1, jd_tt.

The following functions can be used to convert between UTC, UT1 and TT. Note that these functions return times in units of seconds, while JD's are in units of days; take care to convert to days when adjusting a JD.

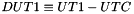ae_dut1() — for calculating $DUT1 \equiv UT1 - UTC$ ;
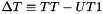ae_delta_t() — for calculating $\Delta T \equiv TT - UT1$ .

Here are some useful constants:

For time conversions: AE_S_PER_D, AE_D_PER_S;
Definitions: AE_J2000, AE_B1950, AE_J1900, AE_MJD_START.

References:

The Astronomical Almanac, Section B., U.S. Government Printing Office, Washington. Published annually.
International Earth Rotation and Reference Systems Service (IERS). Internet URL: http://www.iers.org/.

Ephemerides and Orbital Elements

AEPHEM can calculate the positions and velocities of Solar System bodies using downloadable JPL ephemerides, built-in tables of perturbation coefficients or by naively applying Kepler's laws. These options are discussed in subsections below. All, however, return the body's position rectangular, heliocentric coordinates, in AU. Speeds are returned in the same coordinate system, in AU per day.

Built-In Coefficients and Orbital Elements

The interface for using built-in tables of perturbation coefficients and for naively applying of Kepler's Laws is the same, viz., ae_kepler(). This function accepts as one of its arguments an ae_orbit_t variable. If the member ptable of the ae_orbit_t variable is NULL, ae_kepler() computes the position from the orbital information stored in the other structure members — i, W, w, a, etc. Otherwise, it computes the position using the perturbation coefficients.

Of the application of Kepler's Laws, little need be said here. The curious user may refer to the source code of ae_kepler() which is copiously documented.

Built-in tables of perturbation coefficients are provided for the eight planets, the moon and Pluto. The global ae_orbit_t variables ae_orb_mercury, ae_orb_venus, etc., contain these perturbation coefficient tables and are suitable for passing to ae_kepler(). Additionally, pointers to these global variables are stored in ae_orb_planet, with the indices in the order of the enum ae_ss_bodies_t.

The tables of coefficients were derived by a least squares fit of periodic terms to JPL's DE404 ephemerides. The periodic frequencies used were determined by spectral analysis and comparison with VSOP87 and other analytical planetary theories. The least squares fit to DE404 covers the interval from -3000 to +3000 for the outer planets, and -1350 to +3000 for the inner planets.

The files mer404.c, ven404.c, ... , plu404.c contain numerical tables for computing the J2000 heliocentric ecliptic longitude, latitude, and distance of the indicated planet. Each file includes a table of statistics from a comparison with DE404. Maximum deviations from DE404 are shown, in arcseconds, over each interval of 500 Julian years. The figure tabulated for deviation in radial distance is scaled relative to the mean distance; to convert to astronomical units, multiply by 4.848e-6 times the mean distance in AU.

The lunar ephemeris files mlr404.c and mlat404.c generate positions relative to the mean equinox and ecliptic of date. They assume the DE403 precession constants used in precess.c and the obliquity in epsilon.c. These differ somewhat from DE200 or IAU constants but are thought to be more accurate.

See Appendix A: Perturbation Coefficient File Formats for details on the format of the perturbation table files.

JPL Ephemerides

NASA's Jet Propulsion Laboratory (JPL) publishes ephemerides for the planets and various other objects. These are not distributed with APHEM, but can be freely downloaded from the JPL website: http://ssd.jpl.nasa.gov/. ASCII and binary versions are available and both can be read by aephem.

To use a JPL ephemeris, first initialise with ae_jpl_init() to create an ae_jpl_handle_t variable. One can then use ae_jpl_get_coords() to determine coordinates. Call ae_jpl_close() to free a ae_jpl_handle_t variable.

Astrometric Reductions

Given the position of a Solar System body or a catalogue object, it still remains to compute the apparent position at the centre of the earth.

The functions that performs these computations are described in the sections below. For straightforward applications, however, there are macros which automatically call the necessary reduction functions.

The first class of macros takes an object position and reduces it to its apparent geocentric coordinates in right ascension and declination at the epoch of observation. They are:

ae_geocentric() — you probably do not want to use this more general macro; see the following;
ae_geocentric_from_cat() — reduces a catalogue position, e.g., of a star or galaxy;
ae_geocentric_from_jpl() — reduces a Solar System body given by a JPL ephemeris;
ae_geocentric_from_orbit() — reduces a Solar System body given by the built-in perturbation coefficients or orbital elements.

The second class of macros take a geocentric position and reduces it to its apparent coordinates at a particular location on the surface of the earth. For Solar System objects, the largest correction is for Diurnal Parallax. The macros are:

ae_topocentric() — for fine control over the topocentric correction;
aes_topocentric() — a simplified version of the above.

Here follow descriptions of the astrometric reductions which are provided for by AEPHEM, in the order that they are applied for reducing catalogue or ephemeris coordinates to topocentric apparent coordinates.

Light-Travel Time

This reduction is only necessary for Solar System bodies. It accounts for the fact that due to the finite speed of light, a body being observed from the earth is being seen at its position some minutes in the past, not at its current position. This reduction is sometimes confused with aberration but is in fact seperate: aberration (see below) is due to the velocity of the earth, not the body being observed. There is a small effect due to gravitational retardation from the sun.

The light travel time for the inner planets is on the order of minutes, while for distant planets it can be hours. The size of the correction can be significant; for example, when Venus is near the earth, it is about 50 seconds of arc.

The functions that account for light-travel time are:

ae_light_t_jpl() — for use with JPL ephemerides;
ae_light_t_orbit() — for use with built-in perturbation coefficients or orbital elements.

Light Deflection

This is negligable effect unless the object being observed is near the sun, in which case it is still small (1.8 seconds of arc). However, since it is a simple calculation its inclusion will probably not present a significant computational drawback.

The effect is due to the bending of light in the sun's gravitational field. It is calculated with the function ae_relativity().

Annual Aberration

Annual aberration is the aberration of light due to the motion of the earth normal to the incident light ray. Since it depends on the earth's velocity, the apparent position of an object varies with a period of one year. The maximum shift in apparent position it induces is about 20 seconds of arc.

Use ae_annual_aberration() to correct for annual aberration.

Precession

The tidal interaction of the earth with other Solar System bodies, chiefly the moon and sun, causes its axis of rotation to precess. The period of the precession is about thirty-thousand years. The tidal interactions are complex, and the rotation axis also executes smaller motions on shorter time-scales. These motions are considered separately from precession and are called `Nutation', discussed below. In addition to nutation, there is also polar motion, a more erratic motion on even shorter time scales. Because polar motion is so miniscule it is not included in AEPHEM.

The earth's precession changes the apparent position of celestial objects by about 50 seconds of arc per annum.

The function ae_precess() corrects for precession.

Nutation

Nutation is the `nodding' motion of the earth's axis of rotation due to tidal interactions. It occurs on much shorter time scales than the gross Precession, discussed above. The motion is divided into two components: nutation in longitude acts in the direction parallel to the ecliptic while nutation in obliquity is in the direction perpendicular to the ecliptic.

Nutation is usually expressed as a series. The largest term has a period of 6798 days and amplitudes of 17.2 seconds of arc in longitude and 9.2 seconds of arc in obliquity. The other terms have shorter periods and are significantly smaller.

To calculate the nutation in longitude and obliquity, use ae_nutation_lon_ob(). These values can then be used to correct for nutation using ae_nutate(). To do both these procedures in one step, use aes_nutate().

Diurnal Aberration

Diurnal aberration is caused by the same physics as Annual Aberration, but due to the earth's rotation as opposed to its orbital velocity. It is a much smaller effect, changing the apparent position of an object by no more than a third of a second of arc.

Diurnal aberration can be calculated with ae_diurnal_aberration().

Diurnal Parallax

For objects in the Solar System, diurnal parallax can be an important factor in their apparent postions, because the diameter of the earth subtends a significant angle at AU-scale distances. For example, when Venus is nearest to the earth the size of the diurnal parallax is about a minute of arc. Both the geographic latitude and longitude as well as the altitude of the observer figure in the calculation.

Use ae_diurnal_parallax() to compute diurnal parallax.

Atmospheric Refraction

The refraction of light in the earth's atmosphere increases the apparent altitude of a celestial body. It is a large effect, on the order of several minutes of arc near the horizon, and dozens of seconds of arc even at altitudes of sixty degrees.

AEPHEM provides two atmospheric refraction correction models. For visible bands, use ae_refrac_visible(); for infrared through millimetre, use ae_refrac_ulich().

Summary of Astrometric Corrections

The following table summarises the astrometric corrections provided by AEPHEM and indicates the approximate sizes of their effects.

Correction	Summary	Approximate Size
Light-Travel Time	Due to the finite speed of light, a body is seen at an old position on its orbit, not its current position.	Up to tens of seconds of arc.
Light Deflection	Light rays passing near to the sun are bent by its gravitational field.	Maximum 1.8 seconds of arc.
Annual Aberration	Aberration of light due to the earth's orbital motion.	Up to 20 seconds of arc.
Precession	Precession of the earth's axis of rotation.	About 50 seconds of arc per annum.
Nutation	`Nodding' of the earth's axis of rotation due to tidal interactions with the moon and sun.	Up to 17 seconds of arc.
Diurnal Aberration	Aberration of light due to the earth's rotation.	Less than a third of a second of arc.
Diurnal Parallax	Parallax of nearby objects due to the angle subtended by the earth's diameter.	Up to a minute of arc for nearby planets.
Atmospheric Refraction	Refraction of light in the earth's atmosphere.	Several minutes of arc near the horizon.

Physical Elements

AEPHEM can store physical information on the shapes and rotations of Solar System bodies and make computations using them. Physical information is stored in the struct ae_physical_t—see its documentation for details on how the bodys' shape, size and rotational properties are encoded here.

Data for the planets and Pluto are included in AEPHEM, and are named ae_phys_mercury, ae_phys_venus and so on. They are also pointed to by ae_phys_planet. These data are taken from the IAU 2009 Ephemerides (see References).

Physical data can be used to calculate the sub-observer point with ae_subobs_point() or aes_subobs_point(). The sub-observer point is the point in the centre of the body's disc as seen by the observer, and is expressed in terms of the planet's latitude and longitude. N.B.: Currently, there is a bug in the computation of the sub-observer longitude when compared to the JPL HORIZONS results. Consequently, the value that AEPHEM returns should not be trusted. However, the correct latitude is returned (which is all that is needed for calculating the solid angle, for example).

The sub-observer point is needed to calculate the oblateness of the observed disc (assuming that the body is a spheroid). This in turn is required to calculate solid angle, which can be done with the function ae_disc_solid_angle() or aes_disc_solid_angle().

See the example Solid Angles for a demonstration of how to use physical data.

Catalogue Files

AEPHEM can read from two types of catalogue files. The first type stores orbital parameters for Solar System objects and the second holds the more conventional catalogue information on stars or galaxies. The file suffix for catalogues is generally .cat.

Catalogues are columnated ASCII files. Columns are separated by spaces or tabs. Lines beginning with a hash (#) are comments and are ignored by AEPHEM.

Orbit Catalogue Files

Orbit catalogue files are read in using ae_read_orbit_from_cat(). This function returns an ae_orbit_t object which can then be passed, for example, to ae_geocentric_from_orbit().

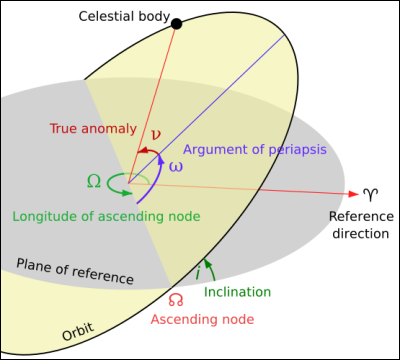
An orbit catalogue file should have twelve columns, containing (in order):

epoch — the Julian Date at which the following data were computed;
inclinataion ( 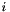) — the angle, in degrees, between the orbital plane and the plane of the ecliptic;
longitude of the ascending node ( 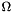$\Omega$ ) — the angle, in degrees, in the plane of the ecliptic between the vernal point ( 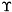$\Upsilon$ ) and the point where the orbit crosses above the ecliptic;
argument of the perihelion ( 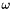$\omega$ ) — the angle, in degrees, in the orbital plane between the longitude of the ascending node and the perihelion (the point in the orbit closest to the sun);
mean distance (or semi-major axis) ( 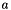) — the distance, in AU, between the centre of the orbit and the perihelion (or, equivalently, the apohelion);
daily motion — this can be omitted from the table (by entering 0) since it is readily calculated from the semi-major axis using Kepler's third law (units are AU per day);
eccentricity ( 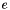) — the eccentricity of the orbit determines the shape of the ellipse;
mean anomoly at epoch ( 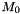) — the angle, in degrees, between the perihelion and the point on the auxiliary circle (i.e., the the circle with the same centre and semi-major axis as the orbital ellipse) at which the planet would be at the epoch;
epoch of equinox and ecliptic — the epoch (in Julian days) at which the equinox ( 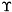$\Upsilon$ ) is defined for these orbital elements;
name — the name of the orbit.

Here is an figure which visualises the orbital elements described above:

Star Catalogue Files

Star catalogue files are read in using ae_read_star_from_cat(). This function returns an ae_star_t object which can then be passed, for example, to ae_geocentric_from_cat().

An star catalogue file should have thirteen columns, containing (in order):

the Gregorian year at which the following data were computed (usually one of 2000 or 1950);
right ascension hour angle;
right ascension minutes;
right ascension seconds;
declination degrees;
declination minutes of arc;
declination seconds of arc;
proper motion in right ascension in seconds of arc per annum ( $\mu_{ra}$ );
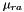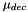proper motion in declination in seconds of arc per annum ( $\mu_{dec}$ );
radial velocity in kilometres per second;
parallax in seconds of arc;
visual magnitude;
the name of the catalogue object.

Constellations

APHEM has built-in knowledge of the constellations. The constellation names are stored in the global array ae_constel_name. The first three characters of an entry in ae_constel_name is the constellation's abbreviation, followed by a space, followed by the full name of the constellation, e.g., "Cap Capricorni". The function ae_cat_to_constel_index() is designed for parsing the catalogue name of a star and determining in which constellation it resides.

The constellation boundaries on the celestial sphere are stored in ae_constel_boundary. Given a right ascension and declination, ae_coord_to_constel_index() determines in which constellation they fall.

Appendix A: Perturbation Coefficient File Formats

Numerical tables for computing the heliocentric ecliptic longitude, latitude and radius of the planets are given in the files mer404.c for the planet Mercury, ven404.c for Venus, etc. Each of these files contains arrays tabl[] of longitude coefficients, tabb[] of latitude coefficients, tabr[] of radius coefficients, and args[] of trigonometric argument harmonics. All the data are organised for efficient access by a computer. In the source files the data are broken up into lines of print, and the order of the lines of arguments in args[] corresponds to the order of the lines of longitude, latitude, and radius coefficients in the other arrays.

In the args table, the first column is the number of items combined to form the trigonometric argument. The next pairs of columns describe the items. The first column of each pair is the harmonic, the second column is the planet number. The last column is the highest polynomial degree of time for this argument.

Thus in mar404.c, the second line of the argument table args[] reads:

3,  4,  3, -8,  4,  3,  5,  2,

The trigonometric argument is the sum of 3 items corresponding to planets 3, 4 and 5 (Earth, Mars and Jupiter). The harmonics are 4, -8, and 3, respectively. Hence the trigonometric argument is

$A = 4 \times [Earth] - 8 \times [Mars] + 3 \times [Jupiter].$

For each planet, the fundamental-frequency angular argument is an initial phase angle plus a frequency multiplied by the time variable. Thus, from the arrays freqs[] and phases[] in the file gplan.c,

$[Earth] = 6890507749.3988 T + 355.43299958 \times 3600.0,$

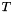where $T$ is in units of 10,000 Julian years from J2000 and the result is measured in arcseconds.

Corresponding to this argument are the amplitude coefficients from the same line of the longitude, latitude, or radius table. The cosine and sine amplitude coefficients of the highest degree term appear first. For the longitude, the complete term corresponding to the second line of coefficients is, from tabl[],

$\left[ \left( 317.74183 \cos A + 730.69258 \sin A \right) T^2 + \left(-15.26502 \cos A + 277.56960 \sin A \right) T + \left(-62.96711 \cos A + 20.96285 \sin A \right) \right] \mathrm{arcseconds} ,$

where, as before,

$A = 4 \times [Earth] - 8 \times [Mars] + 3 \times [Jupiter].$

The first line of args[] lists 0 periodic arguments. This is a special case denoting an expression that is just a polynomial in time. In mar404.c the first line of args[] reads

0,  4,

indicating a 4th degree polynomial in 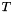$T$ . For the longitude, the coefficients of the polynomial are given in the corresponding line (the first line) of tabl[]. Thus, the complete term is

$43471.66140 T^4 + 21291.11063 T^3 + 2033.37848 + T^2 + 6890507597.78366 T + 1279543.73631,$

in arcseconds, where 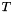$T$ is measured in units of 10,000 Julian years from J2000.

References

The Astronomical Almanac, United States Naval Observatory & Her Majesty's Nautical Almanac Office. Published annually.
Archinal, B.A. et al., "Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009", Celest Mech Dyn Astr 109, 101–135 (2011)
"Nutation and the Earth's Rotation", I.A.U. Symposium No. 78, 1977, p. 256. I.A.U., 1980.
P. Bretagnon and G. Francou, "Planetary theories in rectangular and spherical variables. VSOP87 solutions", Astronomy and Astrophysics 202, 309–315 (1988).
George H. Kaplan, "The IAU Resolutions on Astronomical Reference Systems, Time Scales, and Earth Rotation Models", United States Naval Observatory Circular 179, 2005.
J. Laskar, "Secular terms of classical planetary theories using the results of general theory", Astronomy and Astrophysics 157, 59070 (1986).
J. H. Lieske, T. Lederle, W. Fricke, and B. Morando, "Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants", Astronomy and Astrophysics 58, 1–16 (1977).
J. G. Mangum, "ALMA Memo 366: A Telescope Pointing Algorithm for ALMA", Available at http://www.alma.nrao.edu/memos/html-memos/abstracts/abs366.html.
Roman, Nancy Grace, "Identification of a Constellation from a Position", Pub. Astron. Soc. Pac. 99, 695, (1987).
P. Kenneth Seidelmann (ed.), Explanatory Supplement to the Astronomical Almanac, University Science Books, 1992.
J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touze', G. Francou, and J. Laskar, "Numerical Expressions for precession formulae and mean elements for the Moon and the planets," Astronomy and Astrophysics 282, 663–683 (1994).
Taff, L.G., Celestial Mechanics, A Computational Guide for the Practitioner, Wiley, 1985.
B. L. Ulich, "Millimeter Wave Radio Telescopes: Gain and Pointing Charactersitics", International Journal of Infrared and Millimeter Waves, 2, 2 (1981).
P. A. Wayman (ed.), "Summary of 1980 IAU Theory of Nutation (Final Report of the IAU Working Group on Nutation)", Transactions of the IAU Vol. XVIII A, Reports on Astronomy, D. Reidel Pub. Co., 1982.
James G. Williams, "Contributions to the Earth's obliquity rate, precession, and nutation", Astron. J. 108, 711–724 (1994).
Woolard, E.W., "A redevelopment of the theory of nutation", The Astronomical Journal 58, 1–3, 1953.

Contents

About

Introduction

Quick Example

Conventions

Units

Dates and Times

Ephemerides and Orbital Elements

Built-In Coefficients and Orbital Elements

JPL Ephemerides

Astrometric Reductions

Light-Travel Time

Light Deflection

Annual Aberration

Precession

Nutation

Diurnal Aberration

Diurnal Parallax

Atmospheric Refraction

Summary of Astrometric Corrections

Physical Elements

Catalogue Files

Orbit Catalogue Files

Star Catalogue Files

Constellations

Appendix A: Perturbation Coefficient File Formats

References