Correct for precession. More...

#include <math.h>
#include <stdlib.h>
#include "aephem.h"

Macros
#define	AE_PRECESS_USE_WILLIAMS 1
	Use Williams's coefficients for calculating precession. More...

#define	AE_PRECESS_USE_SIMON 0
	Use Simon's et al coefficients for calculating precession. More...

#define	AE_PRECESS_USE_IAU 0
	Use Lieske's et al IAU coefficients for calculating precession. More...

#define	AE_PRECESS_USE_LASKAR 0
	Use Laskar's IAU coefficients for calculating precession. More...

Functions
void	ae_precess (double jd_tt, double r[], int direction)
	Precess a coordinate. More...

Variables
double	ae_precess_coef []
	Precession coefficients. More...

double	ae_precess_node_coef []
	Precession node coefficients. More...

double	ae_precess_incl_coef []
	Precession inclination coefficients. More...

Detailed Description

Correct for precession.

Macro Definition Documentation

#define AE_PRECESS_USE_IAU 0

Use Lieske's et al IAU coefficients for calculating precession.

Reference:

J. H. Lieske, T. Lederle, W. Fricke, and B. Morando, "Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants," Astronomy and Astrophysics 58, 1-16 (1977).

#define AE_PRECESS_USE_LASKAR 0

Use Laskar's IAU coefficients for calculating precession.

Newer formulas that cover a much longer time span are from:

J. Laskar, "Secular terms of classical planetary theories using the results of general theory," Astronomy and Astrophysics 157, 59070 (1986).

See also:

P. Bretagnon and G. Francou, "Planetary theories in rectangular and spherical variables. VSOP87 solutions," Astronomy and Astrophysics 202, 309-315 (1988).

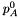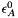Laskar's expansions are said by Bretagnon and Francou to have "a precision of about 1" over 10000 years before and after J2000.0 in so far as the precession constants $p^0_A$ and $\epsilon^0_A$ are perfectly known.

Bretagnon and Francou's expansions for the node and inclination of the ecliptic were derived from Laskar's data but were truncated after the term in 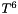$T^6$ . I have recomputed these expansions from Laskar's data, retaining powers up to 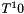$T^10$ in the result.

The following table indicates the differences between the result of the IAU formula and Laskar's formula using four different test vectors, checking at J2000 plus and minus the indicated number of years.

Years from J2000	Arcseconds
0	0
100	0.006
200	0.006
500	0.015
1000	0.28
2000	6.4
3000	38.0
10000	9400.

#define AE_PRECESS_USE_SIMON 0

Use Simon's et al coefficients for calculating precession.

Laskar's terms of order higher than 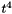$t^4$ have been retained, because Simon et al. mention that the solution is the same except for the lower order terms.

Reference:

J. L. Simon, P. Bretagnon, J. Chapront, M. Chapront-Touze', G. Francou, and J. Laskar, "Numerical Expressions for precession formulae and mean elements for the Moon and the planets," Astronomy and Astrophysics 282, 663-683 (1994).

#define AE_PRECESS_USE_WILLIAMS 1

Use Williams's coefficients for calculating precession.

Laskar's terms of order higher than 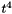$t^4$ have been retained, because Simon et al. mention that the solution is the same except for the lower order terms.

Reference:

James G. Williams, "Contributions to the Earth's obliquity rate, precession, and nutation," Astron. J. 108, 711-724 (1994).

Function Documentation

void ae_precess	(	double	jd_tt,
		double	r[],
		int	direction
	)

Precess a coordinate.

The precession is calcuated using ae_precess_coef, ae_precess_node_coef and ae_precess_incl_coef.

Parameters

jd_tt	The Julian date in TT.
r	A rectangular coordinate vector to be precessed. This routine returns the precessed coordinate in this parameter.
direction	AE_TO_J2000 to precess from `jd_tt` to J2000; AE_FROM_J2000 to precess from J2000 to `jd_tt`. (If neither is passed, AE_TO_J2000 is assumed.) To precess from jd_1 to jd_2, first go from jd_1 to J2000, and then from J2000 to jd_2.

References ae_epsilon(), AE_FROM_J2000, AE_J2000, ae_precess_coef, ae_precess_incl_coef, ae_precess_node_coef, AE_STR, and AE_TO_J2000.

Referenced by ae_coord_to_constel_index(), ae_geocentric(), ae_geocentric_from_cat(), ae_kepler(), ae_kepler_embofs(), ae_phys_pole(), and ae_rect_to_polar_with_jd().

Variable Documentation

double ae_precess_coef[]

Initial value:

= {
      
      -8.66e-10, -4.759e-8, 2.424e-7, 1.3095e-5, 1.7451e-4, -1.8055e-3,
      -0.235316, 0.076, 110.5414, 50287.91959
  }

Precession coefficients.

The exact definition will depend on which of AE_PRECESS_USE_WILLIAMS, AE_PRECESS_USE_SIMON, AE_PRECESS_USE_IAU or AE_PRECESS_USE_LASKAR is set.

Referenced by ae_precess().

double ae_precess_incl_coef[]

Initial value:

= {
    1.2147e-16, 7.3759e-17, -8.26287e-14, 2.503410e-13, 2.4650839e-11, 
    -5.4000441e-11, 1.32115526e-9, -6.012e-7, -1.62442e-5, 0.00227850649, 0.0}

Precession inclination coefficients.

The exact definition will depend on which of AE_PRECESS_USE_WILLIAMS, AE_PRECESS_USE_SIMON, AE_PRECESS_USE_IAU or AE_PRECESS_USE_LASKAR is set.

Referenced by ae_precess().

double ae_precess_node_coef[]

Initial value:

= {
    6.6402e-16, -2.69151e-15, -1.547021e-12, 7.521313e-12, 1.9e-10, -3.54e-9, 
    -1.8103e-7,  1.26e-7,  7.436169e-5, -0.04207794833,  3.052115282424}

Precession node coefficients.

The exact definition will depend on which of AE_PRECESS_USE_WILLIAMS, AE_PRECESS_USE_SIMON, AE_PRECESS_USE_IAU or AE_PRECESS_USE_LASKAR is set.

Referenced by ae_precess().

Macros

Functions

Variables

Detailed Description

Macro Definition Documentation

Function Documentation

Variable Documentation