This file contains functionns for computing physical ephemerides. More...
Functions | |
| double | ae_disc_solid_angle (double a, double b, double dist) |
| Calculate the solid angle of an observed disc. More... | |
| double | aes_disc_solid_angle (double jd_ut1, const struct ae_orbit_t *o_orb, const struct ae_orbit_t *q_orb, const struct ae_physical_t *phys) |
| Calculate the solid angle of an observed disc. More... | |
| double | ae_disc_semiminor (double a, double c, double lat) |
| Calculate the semi-minor axis of an observed disc. More... | |
| int | ae_is_retrograde (const struct ae_physical_t *phys) |
| Determine whether a body's rotation is retrograde. More... | |
| void | aes_subobs_point (double jd_ut1, const struct ae_orbit_t *o_orb, const struct ae_orbit_t *q_orb, const struct ae_physical_t *phys, double *lat, double *lon, double *dist) |
| Calculate the sub-observer point. More... | |
| void | ae_subobs_point (double j[], double n[], double w, double f, int retrograde, double *lat, double *lon) |
| Calculate the sub-observer point. More... | |
| void | ae_phys_pole (double jd_ut1, double jd_tt, const struct ae_physical_t *phys, double n[], double *w) |
| Calculate the axis of a body's north pole and its prime meridean. More... | |
| double | ae_flattening (const struct ae_physical_t *phys) |
| Calculate a body's flattening. More... | |
Detailed Description
This file contains functionns for computing physical ephemerides.
Function Documentation
| double ae_disc_semiminor | ( | double | a, |
| double | c, | ||
| double | lat | ||
| ) |
Calculate the semi-minor axis of an observed disc.
When an oblate spheroid is viewed, it appears as an ellipse (to a sufficiently distant observer). This routine calculates the semi-minor axis (i.e., polar radius) of the projected ellipse.
- Parameters
-
a The major axis (i.e., equatorial radius) of the planet. c The minor axis (i.e., polar radius) of the planet. lat The sub-observer latitude, in degrees.
- Returns
- The semi-minor axis of the projected ellipse. Note that the semi-major axis of the ellipse is the same as the input value.
References AE_DTR.
Referenced by aes_disc_solid_angle().
| double ae_disc_solid_angle | ( | double | a, |
| double | b, | ||
| double | dist | ||
| ) |
Calculate the solid angle of an observed disc.
It is assumed that the disc is elliptical. The semi-minor axis of the projected ellipse can be obtained from ae_disc_semiminor(). Note that this calculation assumes that the size of the disc is small compared to the distance of the observer.
- Parameters
-
a The semi-major axis of the disc, in kilometres. b The semi-minor axis of the disc, in kilometres. dist The distance from the observer to the planet, in AU.
- Returns
- The solid angle of the disc, in steradians.
References AE_AU.
Referenced by aes_disc_solid_angle().
| double ae_flattening | ( | const struct ae_physical_t * | phys | ) |
Calculate a body's flattening.
Takes the equatorial radius,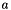 
, and polar radius, 
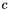, and calculates the flattening of the oblate sphere:
![\[f \equiv \frac{a - b}{a}\]](form_34.png)
- Parameters
-
phys The physical parameters of the body.
- Returns
- The flattening.
References ae_physical_t::r_eq, and ae_physical_t::r_pole.
Referenced by aes_subobs_point().
| int ae_is_retrograde | ( | const struct ae_physical_t * | phys | ) |
Determine whether a body's rotation is retrograde.
This function merely looks at the sign of the variable w_d in the struct ae_physical_t: negative values are retrograde.
- Parameters
-
phys The body to examine.
- Returns
- 1 if the rotation is retrograde; 0 if the rotation is prograde.
References ae_physical_t::w_d.
Referenced by aes_subobs_point().
| void ae_phys_pole | ( | double | jd_ut1, |
| double | jd_tt, | ||
| const struct ae_physical_t * | phys, | ||
| double | n[], | ||
| double * | w | ||
| ) |
Calculate the axis of a body's north pole and its prime meridean.
Get the precessed, nutated direction of the body's north pole; also return the prime meridean.
- Parameters
-
jd_ut1 The Julian date in UT1. For reasonable accuracy, pass a date that has been corrected for light travel time, to get the position of the north pole and meridean as seen by the observer. jd_tt The Julian date in TT. This should not be corrected for light-travel time. phys The physical parameters of the body. n For returning the unit vector of the north pole, in equatorial units of date, in degrees. w For returning the prime meridean, in degrees.
References ae_physical_term_t::a, AE_DTR, AE_FROM_J2000, AE_J2000, ae_mod_360(), AE_PHYSICAL_D, AE_PHYSICAL_END, ae_polar_to_rect(), ae_precess(), aes_nutate(), ae_physical_term_t::b, ae_physical_term_t::c, ae_physical_term_t::d, ae_physical_t::dec_cos_term, ae_physical_t::pole_dec, ae_physical_t::pole_dec_t, ae_physical_t::pole_ra, ae_physical_t::pole_ra_t, ae_physical_t::ra_sin_term, ae_physical_term_t::time_var, ae_physical_t::w, ae_physical_t::w_d, ae_physical_t::w_d_sq, and ae_physical_t::w_sin_term.
Referenced by aes_subobs_point().
| void ae_subobs_point | ( | double | j[], |
| double | n[], | ||
| double | w, | ||
| double | f, | ||
| int | retrograde, | ||
| double * | lat, | ||
| double * | lon | ||
| ) |
Calculate the sub-observer point.
The sub-observer point is the latitude and longitude on an observed body at the observer is directly over-head.
Note that all input values should be precessed and nutated to the epoch of observation.
WARNING: the longitude computed by this function is, for some reason, only accurate to tens of arc minutes when compared to HORIZONS (and I don't know why. Latitude is accurate to a fraction of an arc minute.
- Parameters
-
j The unit vector pointing from the centre of the observed body to the observer. n The unit vector of the north pole of the observed body, in equatorial coordinates of date. w The prime meridean of the observed body, in degreees. f The flattening of the observed body. retrograde Pass non-zero value if the rotation is retrograde, i.e., the body rotates in the opposite sense of the earth's rotation. Pass 0 for prograde rotation. lat For returning the sub-observer latitude, in degrees. lon For returning the sub-observer longitude, in degrees.
References AE_DTR, ae_mod_180(), ae_mod_360(), ae_polar_to_rect(), ae_rect_to_polar(), AE_RTD, ae_zatan2(), ae_physical_t::pole_dec, and ae_physical_t::pole_ra.
Referenced by aes_subobs_point().
| double aes_disc_solid_angle | ( | double | jd_ut1, |
| const struct ae_orbit_t * | o_orb, | ||
| const struct ae_orbit_t * | q_orb, | ||
| const struct ae_physical_t * | phys | ||
| ) |
Calculate the solid angle of an observed disc.
This simplified routine is potentially less efficient, since the distance to the planet is calculated as well as the sub-earth latitude to find the semi-minor axis of the projected disc—ae_disc_solid_angle() and ae_disc_semiminor() can make use of precomputed values.
- Parameters
-
jd_ut1 The Julian date in UT1. o_orb The orbital elements of the observer. q_orb The orbital elements of the object being observed. phys The physical elements of the object being observed.
- Returns
- The solid angle of the disc, in steradians.
References ae_disc_semiminor(), ae_disc_solid_angle(), aes_subobs_point(), ae_physical_t::r_eq, and ae_physical_t::r_pole.
| void aes_subobs_point | ( | double | jd_ut1, |
| const struct ae_orbit_t * | o_orb, | ||
| const struct ae_orbit_t * | q_orb, | ||
| const struct ae_physical_t * | phys, | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | dist | ||
| ) |
Calculate the sub-observer point.
This is a simplified version of ae_subobs_point(). It automatically calculates the requisite unit vectors, given the orbital and physical elements of the bodies.
The sub-observer point is the latitude and longitude on an observed body at the observer is directly over-head.
This routine includes corrections for light-travel time, annual aberration, precession and nutation.
WARNING: the longitude computed by this function is, for some reason, only accurate to tens of arc minutes when compared to HORIZONS (and I don't know why. Latitude is accurate to a fraction of an arc minute.
- Parameters
-
jd_ut1 The Julian date in UT1. o_orb The orbital elements of the observer. q_orb The orbital elements of the object being observed. phys The physical elements of the object being observed. lat For returning the sub-observer latitude, in degrees. lon For returning the sub-observer longitude, in degress. dist For returning the distance to the object, in AU. Set to NULL if you do not require this value. Note that this returns the distance between the centres of the two bodies.
References AE_D_PER_S, ae_delta_t(), ae_flattening(), ae_geocentric(), ae_is_retrograde(), ae_kepler(), ae_light_t(), ae_phys_pole(), ae_polar_to_rect(), ae_subobs_point(), ae_v_orbit(), and ae_physical_t::w.
Referenced by aes_disc_solid_angle().