This file contains functions for calendar and time conversions. More...

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include "aephem.h"

Functions
double	ae_gmst (double jd_ut1, double jd_tt)
	Get the Greenwich mean sidereal time. More...

double	ae_gast (double jd_ut1, double jd_tt, double nutl, double eps)
	Get Greenwich apparent sidereal time. More...

double	ae_lmst (double jd_ut1, double jd_tt, double tlong)
	Get the local mean sidereal time. More...

double	ae_last (double jd_ut1, double jd_tt, double tlong, double nutl, double eps)
	Get the local apparent sidereal time. More...

double	aes_last (double jd_ut1, double tlong)
	Get the local apparent sidereal time. More...

double	ae_tdb (double jd)
	Find Barycentric Dynamical Time from Terrestrial Dynamical Time. More...

double	ae_cal_to_jd (long year, int month, double day)
	Calculate Julian date from a Gregorian calendar date. More...

void	ae_jd_to_cal (double jd, int year, int month, double *day)
	Calculate month, day, and year from a Julian date. More...

double	ae_ctime_to_jd (double t)
	Convert a C time to a Julian date. More...

double	ae_ctime_to_last (double t, double delta_t, double tlong, double nutl, double eps)
	Calculate the local apparent sidereal time from a C time. More...

double	aes_ctime_to_last (double t, double tlong)
	Calculate the local sidereal time from a C time. More...

double	ae_mjd (double jd)
	Given a Julian Date, get the Modified Julian Date. More...

double	ae_delta_t (double jd_ut1)
	Get the value of delta T == Ephemeris Time - Universal Time. More...

double	ae_dut1 (double jd_utc)
	Given a UTC, return DUT1. More...

Variables
short	ae_delta_t_tab []
	A table of delta_T = Ephemeris Time - Universal Time over many years. More...

const int	ae_delta_t_start_year
	The first year of delta T tabulation.

const int	ae_delta_t_end_year
	The final year of delta T tabulation.

const double	ae_dut1_first_mjd
	The Modified Julian Date of the first entry in ae_dut1_tab[].

const double	ae_dut1_last_mjd
	The Modified Julian Date of the last entry in ae_dut1_tab[].

short	ae_dut1_tab []
	A table of DUT1, the difference between UT1 and UTC. More...

const double	ae_dut1_predict_offset
	Offset for predicting DUT1 past the end of ae_dut1_tab[].

const double	ae_dut1_predict_scale
	Scale for predicting DUT1 past the end of ae_dut1_tab[].

const double	ae_dut1_predict_mjd
	Reference MJD for predicting DUT1 past the end of ae_dut1_tab[].

Detailed Description

This file contains functions for calendar and time conversions.

Function Documentation

double ae_cal_to_jd	(	long	year,
		int	month,
		double	day
	)

Calculate Julian date from a Gregorian calendar date.

The Julian date is double precision floating point with the origin used by astronomers.

There is no year 0. Enter B.C. years as negative; i.e., 2 B.C. = -2.

The approximate range of dates handled is 4713 B.C. to 54,078 A.D. This should be adequate for most applications.

B.C. dates are calculated by extending the Gregorian sequence of leap years and century years into the past. This seems the only sensible definition, but it may not be the official one.

Note that the astronomical Julian day starts at noon on the previous calendar day. Thus at midnight in the morning of the present calendar day the Julian date ends in 0.5; it rolls over to tomorrow at noon today.

The month-finding algorithm is attributed to Meeus.

Parameters

year	The Gregorian year.
month	The month of the year, with January = 1, February = 2, etc.
day	The fractional day of the month, starting at 1.

Returns: The Julian day number.

Referenced by ae_ctime_to_jd().

double ae_ctime_to_jd ( double t )

Convert a C time to a Julian date.

The C time is the time since the Epoch (00:00:00 UTC, January 1, 1970), measured in seconds.

Parameters

t	The C time at which to calculate the Julian date.

Returns: The Julian date.

References ae_cal_to_jd(), and AE_STDAY.

Referenced by ae_ctime_to_last(), and aes_ctime_to_last().

double ae_ctime_to_last	(	double	t,
		double	delta_t,
		double	tlong,
		double	nutl,
		double	eps
	)

Calculate the local apparent sidereal time from a C time.

The C time is the time since the Epoch (00:00:00 UTC, January 1, 1970), measured in seconds.

Parameters

t	The UNIX time in UT1 measure at which to calculate the LST.
delta_t	TT - UT1 (see ae_delta_t()), in seconds.
tlong	The longitude of the observer, in degrees.
nutl	The nutation in longitude in seconds of arc (see ae_nutation_lon_ob()).
eps	The obliquity of the ecliptic in seconds of arc (see ae_epsilon()).

Returns: The LAST in degrees.

References ae_ctime_to_jd(), AE_D_PER_S, ae_dut1(), and ae_last().

double ae_delta_t ( double jd_ut1 )

Get the value of delta T == Ephemeris Time - Universal Time.

This routine uses the table ae_delta_t_tab for historic values and near-future predictions.

The program adjusts for a value of secular tidal acceleration ndot. It is -25.8 arcsec per century squared for JPL's DE403 ephemeris. ELP2000 and DE200 use the value -23.8946.

For dates earlier than the tabulated range, the program calculates approximate formulae of Stephenson and Morrison or K. M. Borkowski. These approximations have an estimated error of 15 minutes at 1500 B.C. They are not adjusted for small improvements in the current estimate of ndot because the formulas were derived from studies of ancient eclipses and other historical information, whose interpretation depends only partly on ndot.

A quadratic extrapolation formula, that agrees in value and slope with current data, predicts future values of deltaT.

References:

Stephenson, F. R., and L. V. Morrison, "Long-term changes in the rotation of the Earth: 700 B.C. to A.D. 1980," Philosophical Transactions of the Royal Society of London Series A 313, 47-70 (1984)
Borkowski, K. M., "ELP2000-85 and the Dynamical Time - Universal Time relation," Astronomy and Astrophysics 205, L8-L10 (1988)
- Borkowski's formula is derived from eclipses going back to 2137 BC and uses lunar position based on tidal coefficient of -23.9 arcsec/cy^2.
Chapront-Touze, Michelle, and Jean Chapront, Lunar Tables and Programs from 4000 B.C. to A.D. 8000, Willmann-Bell 1991
- Their table agrees with the one here, but the entries are rounded to the nearest whole second.
Stephenson, F. R., and M. A. Houlden, Atlas of Historical Eclipse Maps, Cambridge U. Press (1986)

Parameters

jd_ut1 The Julian date.

Returns: The ET - UT (delta T) in seconds.

References ae_delta_t_end_year, ae_delta_t_start_year, ae_delta_t_tab, and AE_J2000.

Referenced by aes_last(), aes_subobs_point(), and aes_topocentric().

double ae_dut1 ( double jd_utc )

Given a UTC, return DUT1.

DUT1 is the offset between UTC and UT1, i.e., 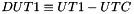$DUT1 \equiv UT1 - UTC$ . Functions that find sidereal time expect UT1, so this function will be required to convert UTC if reasonable precision (better than roughly 10 seconds of arc).

Values are taken from a look-up table. Past values start on 19 May 1976 are are tabulated daily until the release date of this version of aephem. After this, predicted values are used through about one year.

If DUT1 is requested for a date before the tabulation starts, 0 will be returned. After the last predicted value, a value will be estimated using an interpolation formula.

Past values, predicted values and the interpolation formula were taken from the U.S. Naval Observatory IERS Bulletin A. This is available online at http://maia.usno.navy.mil/.

Parameters

jd_utc The Julian date in UTC.

Returns: DUT1, in seconds. If jd_utc is before the first tabulated value, 0 will be returned.

References ae_dut1_first_mjd, ae_dut1_last_mjd, ae_dut1_predict_mjd, ae_dut1_predict_offset, ae_dut1_predict_scale, ae_dut1_tab, and ae_mjd().

Referenced by ae_ctime_to_last(), and aes_ctime_to_last().

double ae_gast	(	double	jd_ut1,
		double	jd_tt,
		double	nutl,
		double	eps
	)

Get Greenwich apparent sidereal time.

The Greenwich apparent sidereal time is the Greenwich mean sidereal time corrected for nutation. See ae_gmst() for reference.

Parameters

jd_ut1	The Julian date, in UT1.
jd_tt	The Julian date, in TT. (See ae_delta_t().)
nutl	The nutation in longitude in seconds of arc (see ae_nutation_lon_ob()).
eps	The obliquity of the ecliptic in seconds of arc (see ae_epsilon()).

Returns: Greenwich apparent sidereal time in degrees.

References ae_gmst(), ae_mod_360(), AE_STD, and AE_STR.

Referenced by ae_last().

double ae_gmst	(	double	jd_ut1,
		double	jd_tt
	)

Get the Greenwich mean sidereal time.

Get the mean sidereal time at Greenwich (i.e., longitude 0). The mean sidereal time does not include nutation corrections. Coefficients are from the IAU and can be found in:

George H. Kaplan, "The IAU Resolutions on Astronomical Reference Systems, Time Scales, and Earth Rotation Models," United States Naval Observatory Circular No. 179, 2005.

Parameters

jd_ut1	The Julian date, in UT1.
jd_tt	The Julian date, in TT. (See ae_delta_t().)

Returns: The Greenwich mean sidereal time, in degrees.

References AE_J2000, ae_mod_360(), and AE_STD.

Referenced by ae_gast(), and ae_lmst().

void ae_jd_to_cal	(	double	jd,
		int *	year,
		int *	month,
		double *	day
	)

Calculate month, day, and year from a Julian date.

Parameters

jd	A Julian day number.
year	For returning the year of `jd`.
month	For returning the month of `jd`, in the range [1:12].
day	For returning the fractional day of `jd`, with the first day of the month being 1.

double ae_last	(	double	jd_ut1,
		double	jd_tt,
		double	tlong,
		double	nutl,
		double	eps
	)

Get the local apparent sidereal time.

The local apparent sidereal time is simply the Greenwich apparent sidereal time plus the local longitude. See ae_gast().

Parameters

jd_ut1	The Julian date in UT1.
jd_tt	The Julian date in TT. (See ae_gast().)
tlong	The longitude of the observer in degrees.
nutl	The nutation in longitude in seconds of arc (see ae_nutation_lon_ob()).
eps	The obliquity of the ecliptic in seconds of arc (see ae_epsilon()).

Returns: Local sidereal time in degrees.

References ae_gast(), and ae_mod_360().

Referenced by ae_ctime_to_last(), ae_topocentric(), and aes_last().

double ae_lmst	(	double	jd_ut1,
		double	jd_tt,
		double	tlong
	)

Get the local mean sidereal time.

The local mean sidereal time is simply the Greenwich mean sidereal time plus the local longitude. See ae_gmst().

Parameters

jd_ut1	The Julian date in UT1.
jd_tt	The Julian date in TT. (See ae_delta_t().)
tlong	The longitude of the observer in degrees.

Returns: Local sidereal time in degrees.

References ae_gmst(), and ae_mod_360().

double ae_mjd ( double jd )

Given a Julian Date, get the Modified Julian Date.

The difference between the two is simply a constant, AE_MJD_START.

Returns: The Modified Julian Date.

References AE_MJD_START.

Referenced by ae_dut1().

double ae_tdb ( double jd )

Find Barycentric Dynamical Time from Terrestrial Dynamical Time.

See AA page B5.

Parameters

jd	A Julian date, in TDT.

Returns: The corresponding time in TDB.

References AE_J2000, and AE_STR.

double aes_ctime_to_last	(	double	t,
		double	tlong
	)

Calculate the local sidereal time from a C time.

This is a simplification of ae_ctime_to_last(). It automatically does the calculations of delta_t, nutl and eps. Use ae_ctime_to_last() for more efficiency, especially with repeated calls.

Parameters

t	The UNIX time at which to calculate the LST.
tlong	The longitude of the observer, in degrees.

Returns: The LAST in degrees.

References ae_ctime_to_jd(), AE_D_PER_S, ae_dut1(), and aes_last().

double aes_last	(	double	jd_ut1,
		double	tlong
	)

Get the local apparent sidereal time.

This is a simplified version of ae_last(), which automatically calculates jd_tt, nutl and eps. It might be less efficient to use this routine if speed is required.

Parameters

jd_ut1	The Julian date in UT1.
tlong	The longitude of the observer in degrees.

Returns: Local sidereal time in degrees.

References AE_D_PER_S, ae_delta_t(), ae_epsilon(), ae_last(), and ae_nutation_lon_ob().

Referenced by aes_ctime_to_last().

Variable Documentation

short ae_delta_t_tab[]

A table of delta_T = Ephemeris Time - Universal Time over many years.

There is one value for each year, starting at #ae_delta_t_start_yearand ending at ae_delta_t_end_year.

The tabulated range is 1620.0 onwards. The values from 1620 to 1973 were taken from The Astronomical Almanac, page K8. The values from 2004 onwards (including future projections) are taken from http://maia.usno.navy.mil. Bessel's interpolation formula is implemented to obtain fourth order interpolated values at intermediate times.

Updated deltaT predictions can be obtained from this network archive:

http://maia.usno.navy.mil

N.B.: Stephenson and Morrison's table starts at the year 1630. The Chapronts' table does not agree with the Almanac prior to 1630. The actual accuracy decreases rapidly prior to 1780.

Referenced by ae_delta_t().

short ae_dut1_tab[]

A table of DUT1, the difference between UT1 and UTC.

The entries are in tenths of milliseconds, beginning at the Modified Julian Date given by ae_dut1_first_mjd and incrementing every day thereafter. This format was chosen to minimise the amount of disc space used since short integers can be employed.

The last year of the table consists of forecasted values.

These data were taken from past IERS Bulletin A tables. Values can be found online at http://maia.usno.navy.mil/search/search.html; the file finals.all compiles all values since 1973.

Referenced by ae_dut1().

Functions

Variables

Detailed Description

Function Documentation

Variable Documentation